这个公式背后是一个与赌博有关的故事，收藏级好文

文：知乎日报

凯利公式的前世今生

LIKE，Software Engineer

爱好博彩业和投资学的同学应该都对著名的凯利公式不陌生。这是一个通过计算 edge 和 odds 来选择最佳投注比例的公式，目的是长期获得最高的盈利。

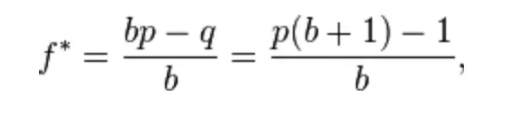
公式中

f = 应该放入投注的资本比值

p = 获胜的概率

q = 失败的概率

b = 赔率

其实公式的作者，John Larry Kelly，并不是一个资深赌徒，而是一位著名的物理学家，他发明这个公式的时候正是著名的 AT&T 的 Bell Lab 中的一名研究科学家，研究方向是当时还算新兴前沿的电视信号传输协议。

这样一个理论科学家是如何把名字和博彩联系在一起的呢？那就不能不看下这本书了。

William PoundStone, 把 Kelly 公式和它发明者的故事写入了他的作品，Fortune’s Formula, the untold story of the scientific betting system that beat the casinos and Wall Street.

1955 年 6 月，美国出现了一个极其有名的电视节目，叫做 64000 dollar question. 答题者通过不断答对题来累积奖金，一时风靡全美，黄金时段收视率达到 85%，各路山寨节目不断。

这样一个 quiz show 迅速吸引了场外下注来赌赢家的赌盘。这档节目的录制是在纽约，东海岸现场直播，而西海岸则有延时。当时的新闻爆出一些丑闻，有关西海岸的赌徒通过电话提前得知结果，赶在了西海岸直播前下注。

John Kelly 看了新闻之后，他想到这个如何使具备一定内幕消息 (private wire) 但是同时有一部分杂音 (noise) 的赌徒最大化长期获益的问题，可以使用他们实验室关于咨询学和噪音传递研究的公式来解决。于是，他以一个赛马的模型，推出了凯利公式的雏形。

John Kelly 的理论是这样的，对于有一定 private wire 的赛马人来说，第一个自然的想法当然是放入全部的资金，但是这样就会造成万一输掉血本无归的惨境。而在 Kelly 想要解决的这个问题中，在任何一个时刻输掉全部资金显然是不符合最大化累积收益的需求的。

真正应该关心的是长期累积的收入 (compounding return)，对于累积的收益来说，最后的结果只和输赢的局数有关，而和输赢的顺序无关。所以他推出了一个最佳的投入仓位比，来最大化长期的累积收益：

bet = edge / odds = 预期获益／获益回报

这里的 edge 在赌博中可以理解为获胜的概率＊赔率 – 失败的概率，当 edge 的数字为正的时候，这就是值得下注的比赛，而 edge 为 0 或者负数的情况说明赌徒不具备 edge, 不应该下注 (applies to most of games in casino)

而 odds 则是赔率，我们更可以把它理解为一种公众对概率的估计，是公开的消息。

我们可以用 kelly formula 模拟这样一种情况：小明现在有 100 元的起始资金，他现在将要投硬币 4 次，每一次他投出硬币为正面的时候，将获得 6 倍资金回报（1 赔 5），当他投出硬币为反面，陪光。

请问小明要如何分配每次下注资金，才能最大化他 4 次投币之后的收益 (maximize geometric mean) 呢？

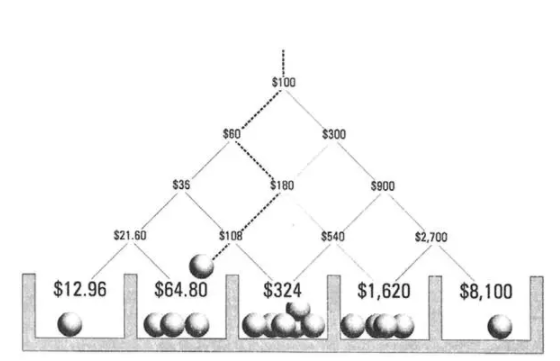
根据 Kelly 公式计算，我们可以建立起这样一个 pascal triangle 正反面的概率各为 50%，edge = 0.5*5-0.5 = 2, odds 为 5，最佳仓位为 40%，可以看到最终在 16 个可能出现的结果中 (4 次投掷)，12.96 和 8100 出现 1 次，64.8 和 1620 出现 4 次，324 出现 6 次，16 次结果的 geometric mean 为 324 – Kelly 公式的目的正是最大化这些结果的 geometric mean。

由于 Kelly 公式着眼于长期回报率和风险的控制，所以天然就吸引投资人想要把它应用在投资当中。

比如著名的传奇数学家 Edward Thorp 读了 John Kelly 的论文之后，先是自学 Fortran 用 IBM 大型机开发了一套专门用于 21 点的算法（感兴趣的同学可以去看下电影 21，电影里的 card counting 的方法正是获得 edge 的来源），带上 John Kelly 的导师在拉斯维加斯大把吸金。

（趁机放张帅帅的 Jim Sturgess 有木有 >.<）

之后又专门成立了一个 hedge fund – Princeton Newport Partners. 看看这个 fund 的表现吧

Kelly Formula 到底在投资中起到了哪些作用，又有哪些可以研究发掘的领域呢？

Kelly Formula 在仓位控制中的应用

在股票市场中，kelly formula 的形式和赌博中稍有不同，因为失败之后有一个 expected loss, 我们将公式修改为 f = (bp – cq) / (bc)，来做一个简单的回测。

假定赚钱 (p) 赔钱概率 (q = 1-p) 一样，均为 0.5，我们认为净赢率 (b) 为最高价 / 当前价 -1，净损失率 (c) 为 1- 最低价 / 当前价。

如果当前价大于一年内最高价，满仓，如果当前价小于一年内最低价，空仓，其他情况使用之前得到的 f 计算出持仓比例(0-1 之间)，每周调仓。

我们挑选了单只股票作回测，回测的参照物是该股票的买入持有策略（即为价格曲线），看看使用 Kelly 公式调节仓位有什么样的效果。

在此基础上，我们再尝试一些优化，

p=q=0.5 的假设太简单粗暴啦，我们来根据历史数据统计过去一年中 5 个交易日内的涨跌概率。

加入新的标准，统计过去一年内该股票的一周最大涨跌幅，以此计算 b 和 c，得到的 f 与之前 f 的求平均。

设定止损。如果一周内跌幅超过 8%，则清仓。

看看是不是优化以后的代码会有更好的表现呢？

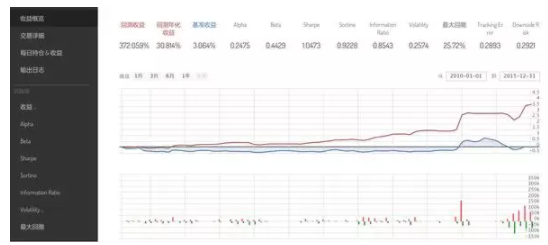
有兴趣的同学可以在这里克隆代码 Kelly Formula 的仓位控制（https://www.ricequant.com/community/topic/598/kelly-formula-简单应用）

Kelly Formula 在选股和建立投资组合方面的应用

Kelly 公式在投资组合的应用中，也经常以 f = excess return/variance 的形式出现，f 的数值越高也就是投资的价值越大：

1. 计算股票池中每只股票的 Kelly leverages 作为排序 score（这里过去一年内每日收益的 mean/var）

2. 从大到小进行排序，选出前 10 名的股票，价格在 5 日均线之上时才购买，平均购买，每月调仓。

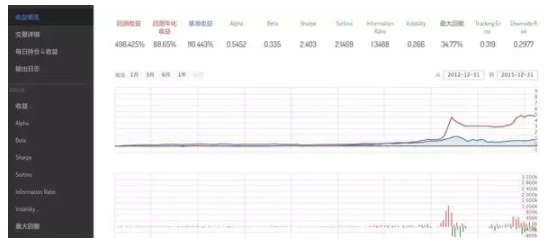
在此基础上仍然有进步的空间，因为我们通过 kelly score 选择股票的时候并未考虑之间的相关性，可以考虑在筛选出股票之后用 covariance matrix 重新计算 kelly 仓位并按照计算仓位比值来调仓。

有兴趣的朋友可以自己克隆现在的策略 Kelly Formula 选股 （https://www.ricequant.com/community/topic/611/kelly-criterion进行选股/2）来进一步优化。

John Larry Kelly (1923 – 1965) 42 岁的时候就不幸去世了，我猜想对于他个人来说，更希望被人铭记的不是拉斯维加斯赌场和 hedge fund 之类的掘金工具，而是他作为科学家最骄傲的一个时刻－ 1961 年，和同事 Gertsman 一起，在 Bell Lab 用 IBM704 合成了人工声音（Synthesize Speech），Kelly 的 vocoder 制作了歌曲 Daisy Bell. 史上第一首由电脑合成的音乐.

就在这一年，一个叫做 Arthur Clarke 的作家访问了 Bell Lab, 被这个人工合成的声音和音乐震惊，将这一幕写入了他的科幻小说。

又过了七年，一个叫做 Kubrike 的导演让一台濒死的电脑 HAL 在科幻电影里把这首歌曲唱了出来，这是对科学家 Kelly 最好的致敬和缅怀。

这部电影就是 2001: A Space Odyssey